

Tools for Fluid Calculations and Simulation Sensing the pressure drop across an air filter minimizes unnecessary power consumption by motors.
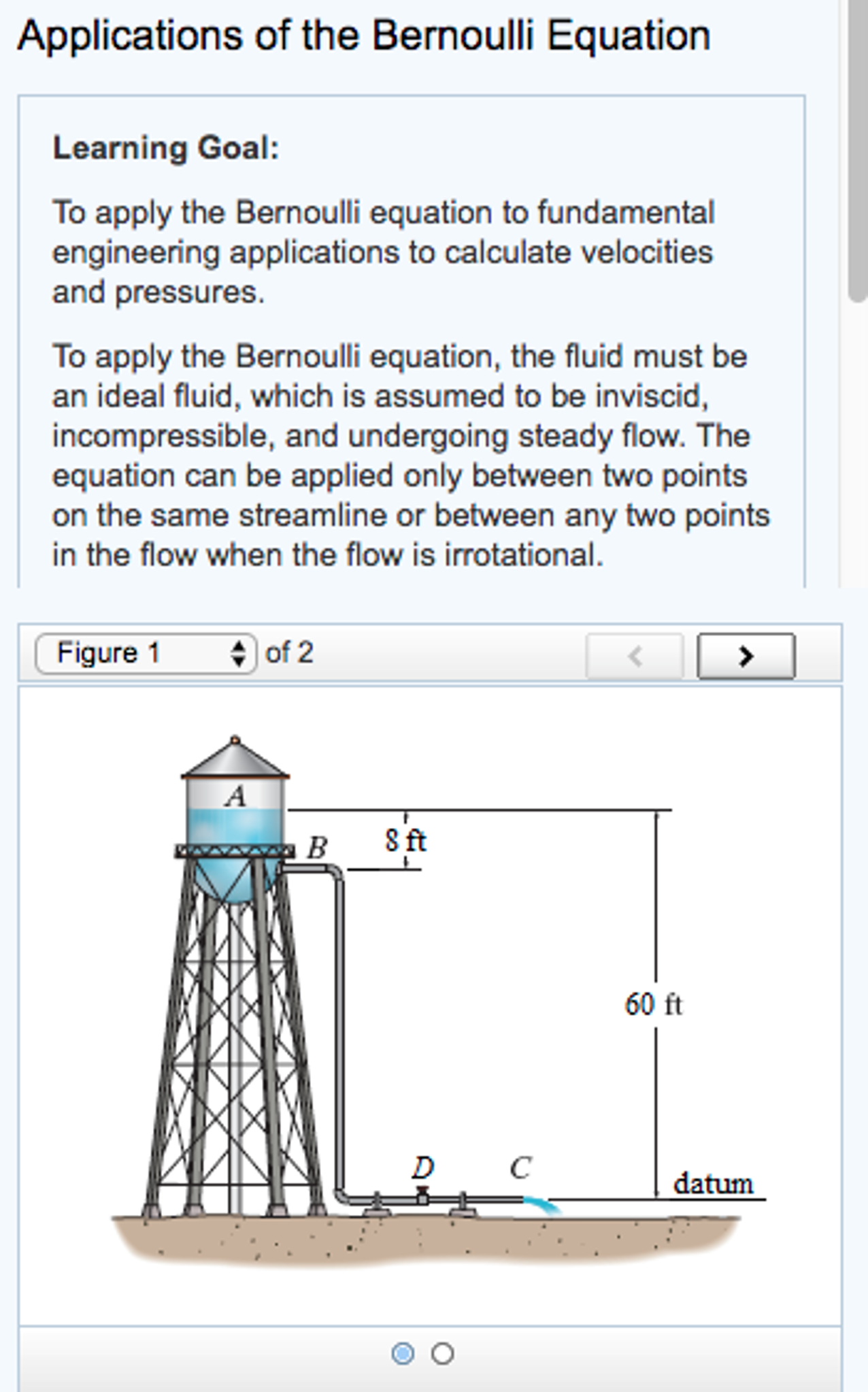
The American Society of Heating, Refrigerating and Air-Conditioning Engineers’ (ASHRAE’s) minimum efficiency reporting value, or MERV rating, measures the effectiveness of air filters. Normal operating pressures are typically in the range of 0.1 to 1” H 2O. In either case, the values are quite low and the pressure measurement requires special consideration in the pressure sensor to achieve the desired accuracy and precision.Ĭlean and low power consumption in heating, ventilation and air conditioning (HVAC) systems require the proper air filters and frequently monitoring to identify a filter that requires changing. For example, the differential pressure in a spirometer or respirator is nominally 4 kPa and in a ventilator, it is nominally 25 cm H 2O. In the medical area, respiratory issues require airflow measurements for ventilator flow/control, and analysis, such as spirometers, as well as gas and liquid flow measurements for treatment. Where E B is the bulk modulus of fluid in psf and ρ is the density of the fluid. The Joukowski impulse equation is used to calculate the resulting pressure when the liquid velocity that drops to zero upon contacting a closed valve.įor rigid pipes, the celerity of the pressure wave or wave speed, c, is found by: Water hammer is the shock caused by the sudden decrease in velocity of a flowing fluid and the time it takes for the pressure wave for round trip travel in the pipe. A Pitot-static or Prandtl tube used to measure aircraft velocity.
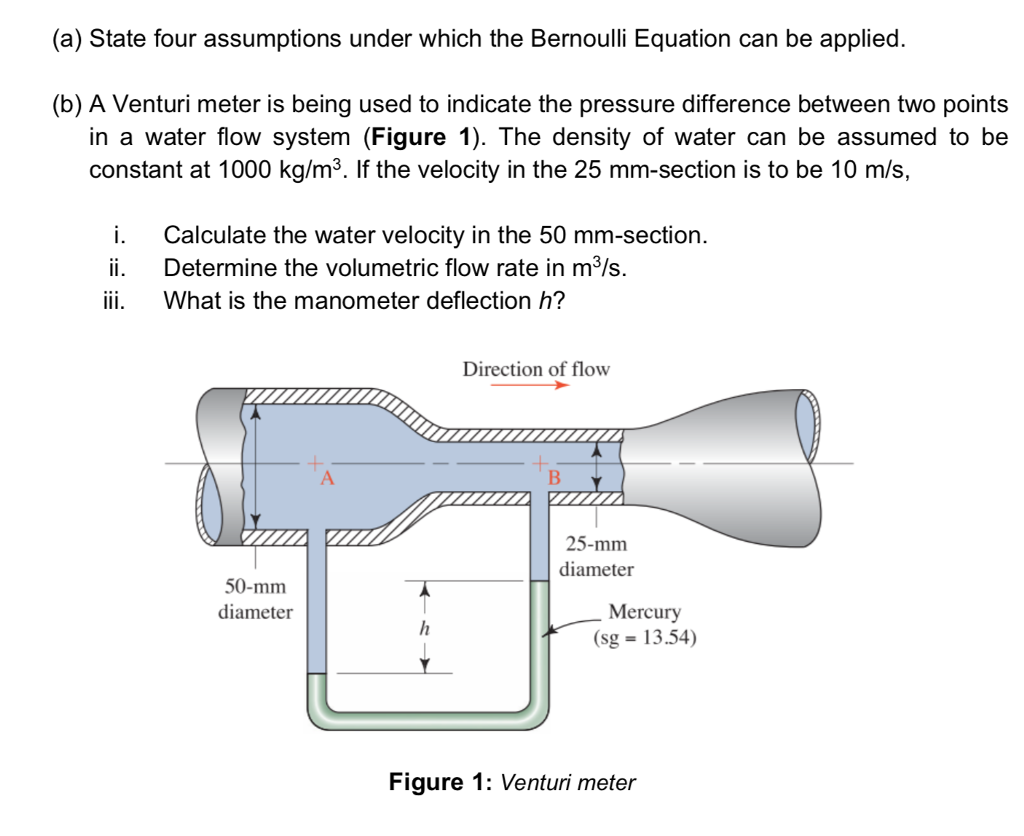
A Pitot-static tube for measuring aircraft velocity is shown in Figure 2.įigure 2. Pitot tubes use the difference between total pressure and static pressure to calculate the velocity of the aircraft or fluid flowing in the pipe or enclosure. P1"> D 1 is the upstream and downstream pipe diameter (in m)įigure 1. Q = c d π/4 D 2 2 1/2Ĭ D is the discharge coefficient, the area ratio = A 2 / A 1ĭ 2 is the orifice, venturi or nozzle inside diameter (in m) In these cases (refer to Figure 1), the flow is related to ΔP (P 1-P 2) by the equation: Orifice plates, Venturi tubes and nozzles simplify the situation. Several factors determine the pressure drop that occurs in fluid flow applications including laminar versus turbulent flow, the flow velocity, kinematic viscosity and Reynolds number of the fluid, internal roughness of the inside of the pipe as well as its diameter, length and form factor. Common types of restrictions include orifice plates, Venturi tubes, nozzles and any structure that has an easily measured pressure differential.įlow in a Pipe/Tube. The Venturi meter is an application of Bernoulli’s equation. The Venturi effect is increase in velocity that occurs when fluid flow is restricted. It starts with qualifications of nonviscous, steady, incompressible flow at a constant temperature. Unlike compressible flow where the density changes with the applied pressure, with incompressible flow, the density is constant in space and time.īernoulli’s Equation is used to determine fluid velocities through pressure measurements. More viscous fluids tend to have laminar flow and a lower Reynolds number. A mixture of laminar and turbulent flow, called transitional flow, occurs in pipes and other enclosures with turbulence in the center of the enclosure, and laminar flow near the edges. With turbulent flow, random motion can result in eddies and other less predictable behavior. In laminar flow, the particle motion is very uniform/orderly and results in straight lines parallel to the enclosure’s walls and is very predictable. Viscous flow results in energy loss (and subsequently a temperature rise) but ideal fluids have nonviscous flow with no energy loss. It is a function of the inertia force (ρ u L), and the viscous or friction force (μ). Reynolds number (Re) is a dimensionless velocity value used to predict flow patterns. The active links in the following sections provide more details. Fluid dynamics provides the means of understanding the parameters that impact fluid flow. Pressure Point 11: Calculating Flow Rate from Pressure Measurementsįluid flow occurs with the motion of liquid and gaseous materials and pressure sensors play a critical role in determining many aspects of fluid flow. All Sensors Pressure Points are application tips to simplify designing with microelectromechanical systems (MEMS) pressure sensors and avoiding common pitfalls.


 0 kommentar(er)
0 kommentar(er)
